251 honeycomb
| 251 honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform tessellation |
| Family | 2k1 polytope |
| Schläfli symbol | {3,3,35,1} |
| Coxeter symbol | 251 |
| Coxeter-Dynkin diagram | |
| 8-face types | 241 {37} |
| 7-face types | 231 {36} |
| 6-face types | 221 {35} |
| 5-face types | 211 {34} |
| 4-face type | {33} |
| Cells | {32} |
| Faces | {3} |
| Edge figure | 051 |
| Vertex figure | 151 |
| Edge figure | 051 |
| Coxeter group | 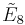 , [35,2,1] , [35,2,1] |
In 8-dimensional geometry, the 251 honeycomb is a space-filling uniform tessellation. It is composed of 241 polytope and 8-simplex facets arranged in a demiocteract vertex figure. It is the final figure in the 2k1 family.
Construction
It is created by a Wythoff construction upon a set of 9 hyperplane mirrors in 8-dimensional space.
The facet information can be extracted from its Coxeter-Dynkin diagram.
Removing the node on the short branch leaves the 8-simplex.
Removing the node on the end of the 5-length branch leaves the 241.
The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes the 8-demicube, 151.
The edge figure is the vertex figure of the vertex figure. This makes the rectified 7-simplex, 051.
See also
References
- Coxeter The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 978-0-486-40919-1 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
- Coxeter Regular Polytopes (1963), Macmillian Company
- Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (Chapter 5: The Kaleidoscope)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]